Вы точно человек?
При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин. Довольно часто дополнительно требуется, чтобы таких классов было наименьшее число. В теории графов подобные задачи формулируются в терминах раскраски вершин графа. Параграф посвящен доказательству утверждения о том, что любой плоский граф можно раскрасить пятью красками теорема 5. Предварительно установим следующий результат.

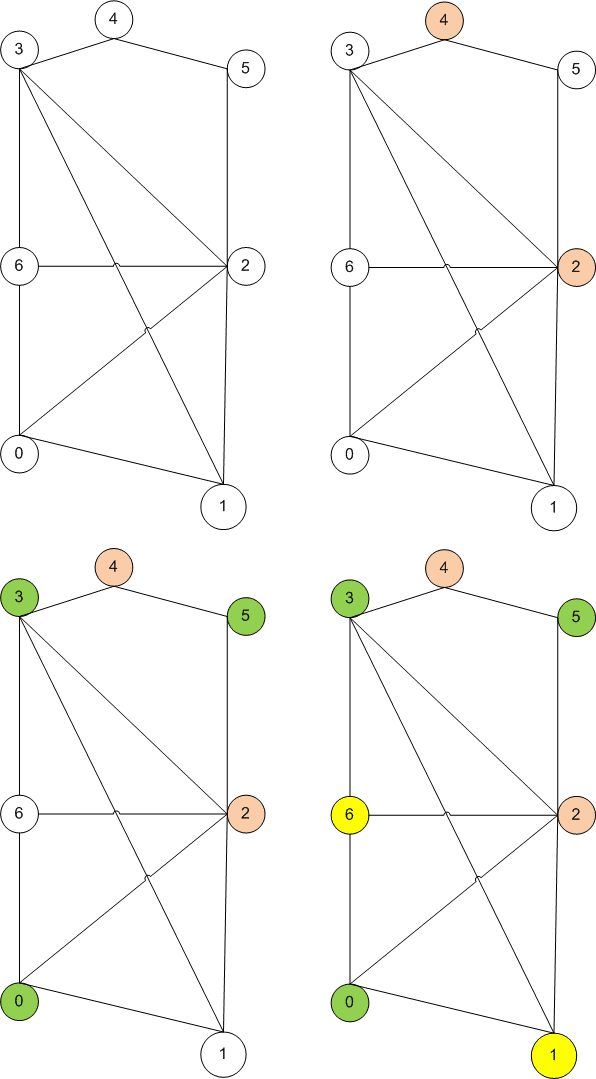


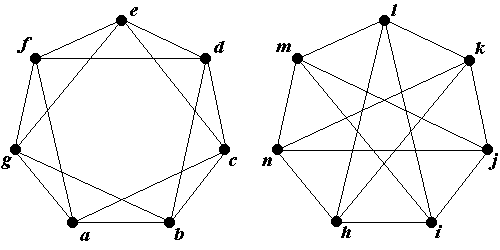
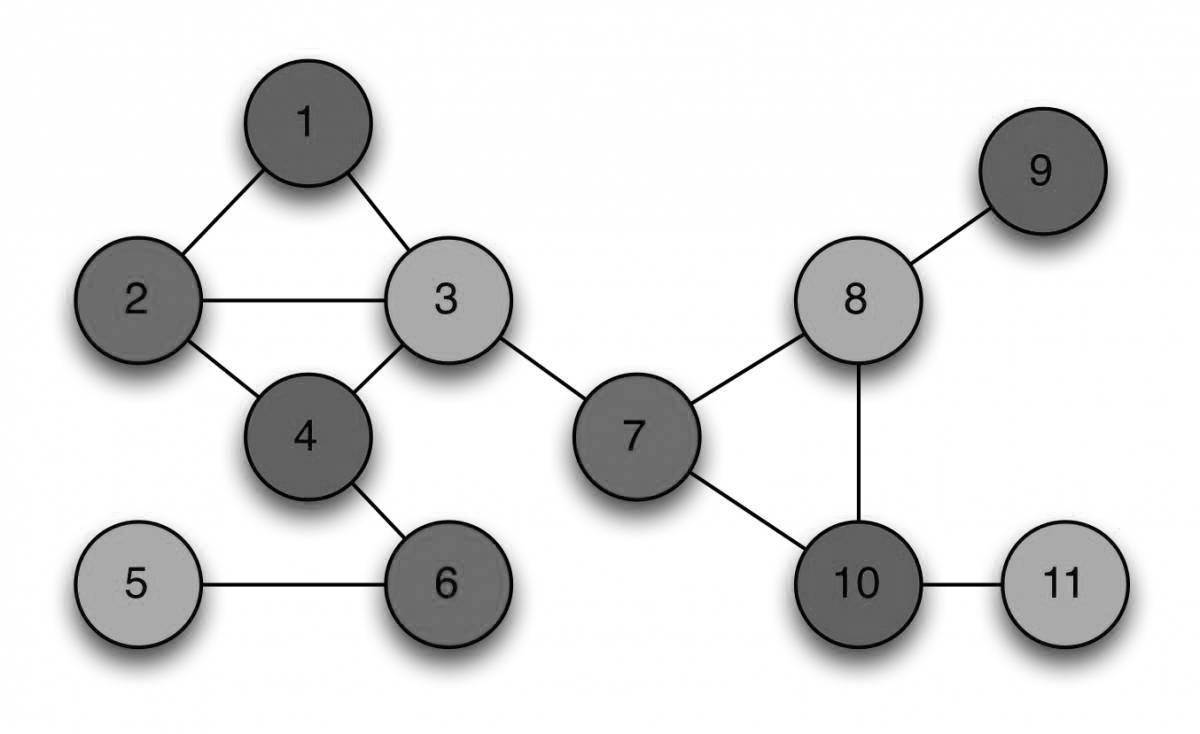

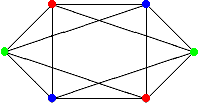
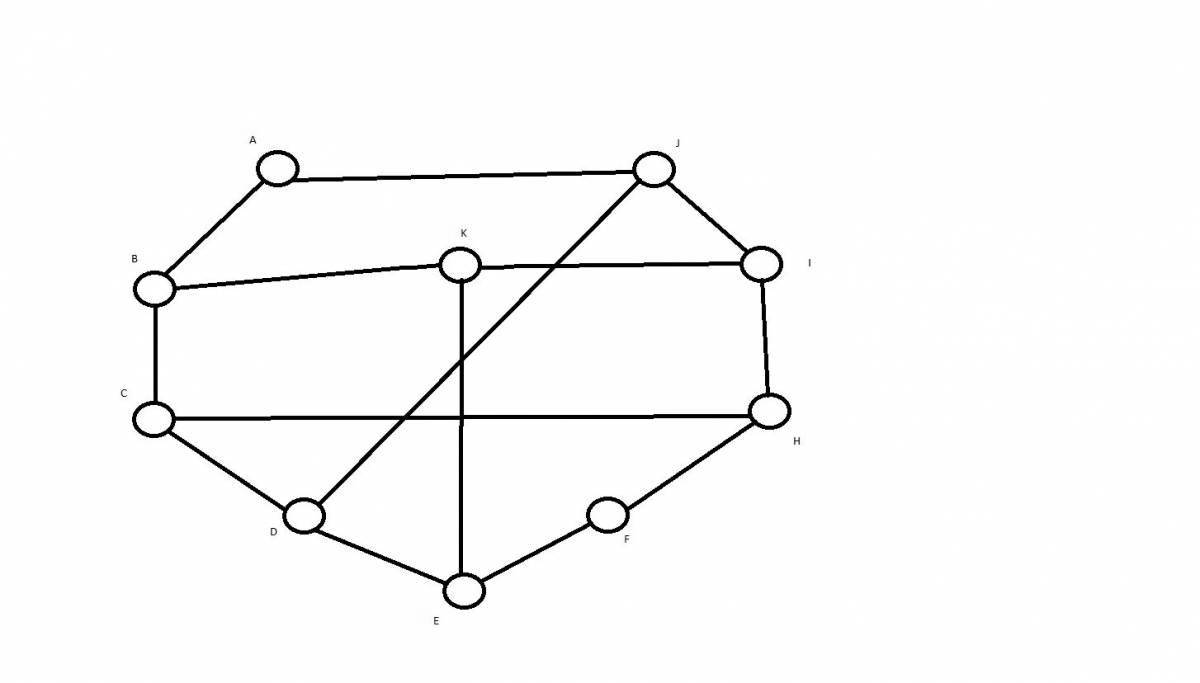




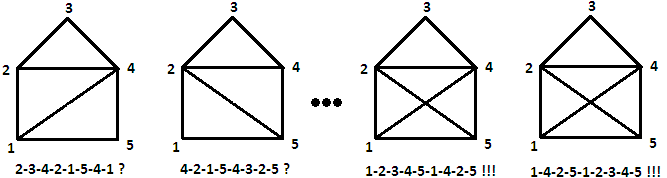
Практическое применение раскраски графов
Графики из дискретной математики — отличный способ визуализировать данные и отношения между различными элементами. Страницы-раскраски с этими графиками могут помочь детям узнать о предмете в веселой и увлекательной форме. Они могут раскрашивать различные элементы графика и узнавать о различных отношениях между ними.
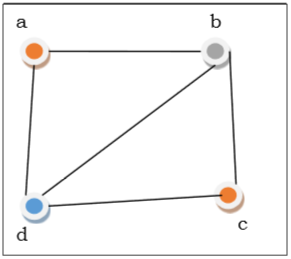
- Характерным специфическим направлением теории графов является цикл задач, связанный с раскраской графов, в котором изучаются разбиения множества вершин ребер , обладающие определенными свойствами, например, смежные вершины ребра должны принадлежать различным множествам вершины или ребра из одного множества окрашиваются одним цветом. Раскраска графов связана с историей возникновения теории графов и так называемой задачей о четырех красках.
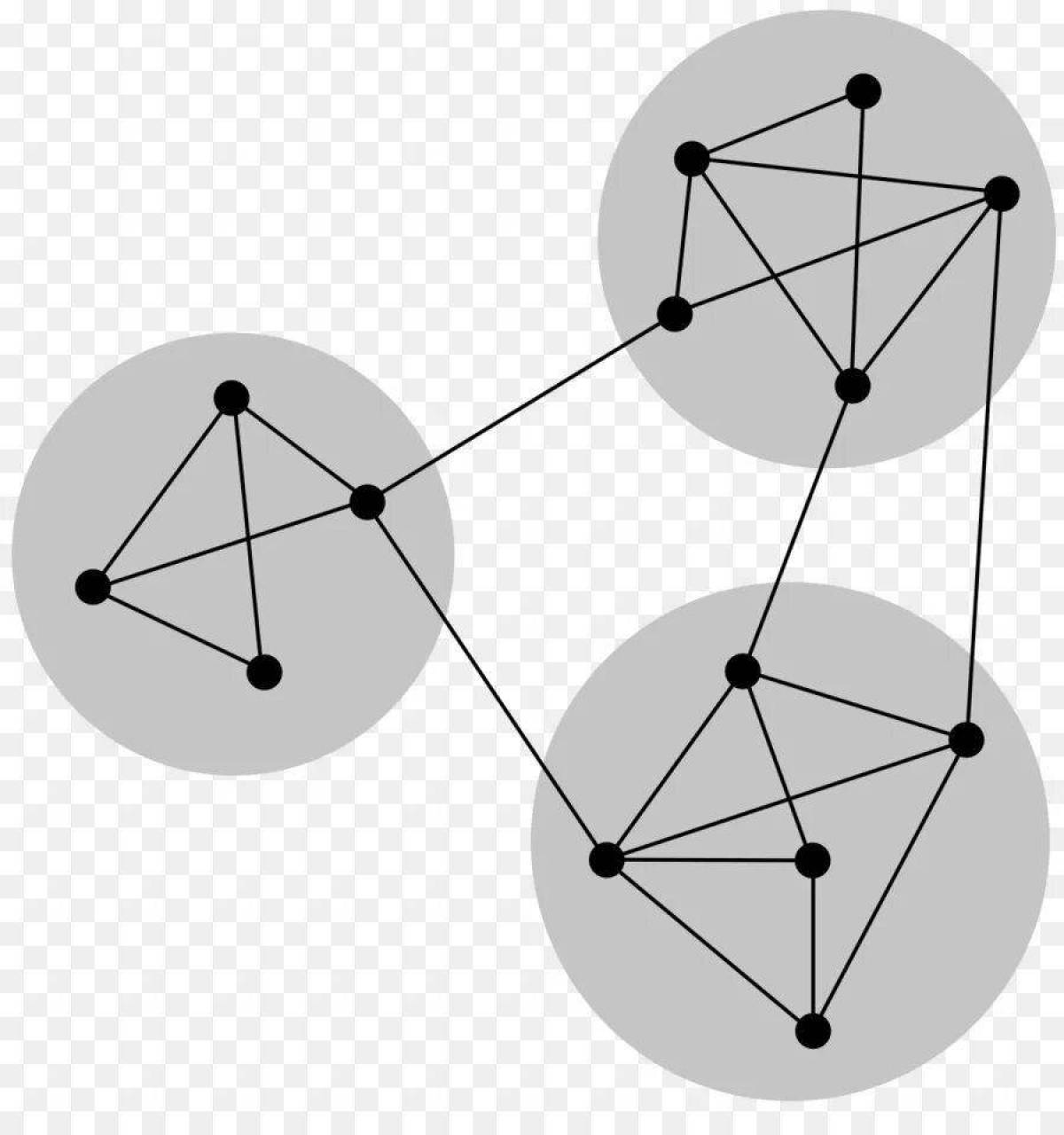
- Независимое множество вершин S внутреннее устойчивое подмножество - это такое подмножество вершин, в котором ни одна из вершин несмежная с любой другой вершиной данного множества.
- Работа выполнена на кафедре высшей математики факультета прикладной матсматики-процессов управления Санкт-Петербургского государственного университета.
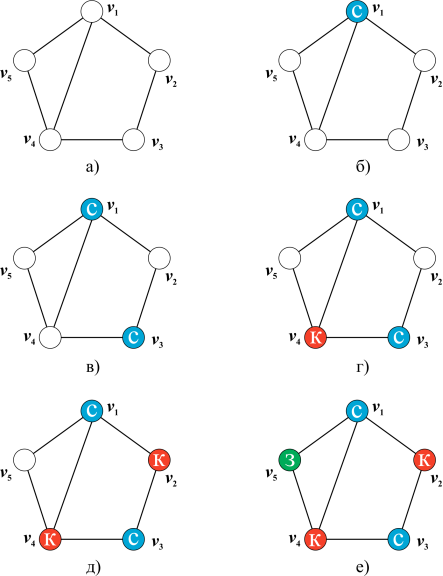
- Рассматриваемый метод раскраски графа является приближенным, достаточно простым и эффективным.
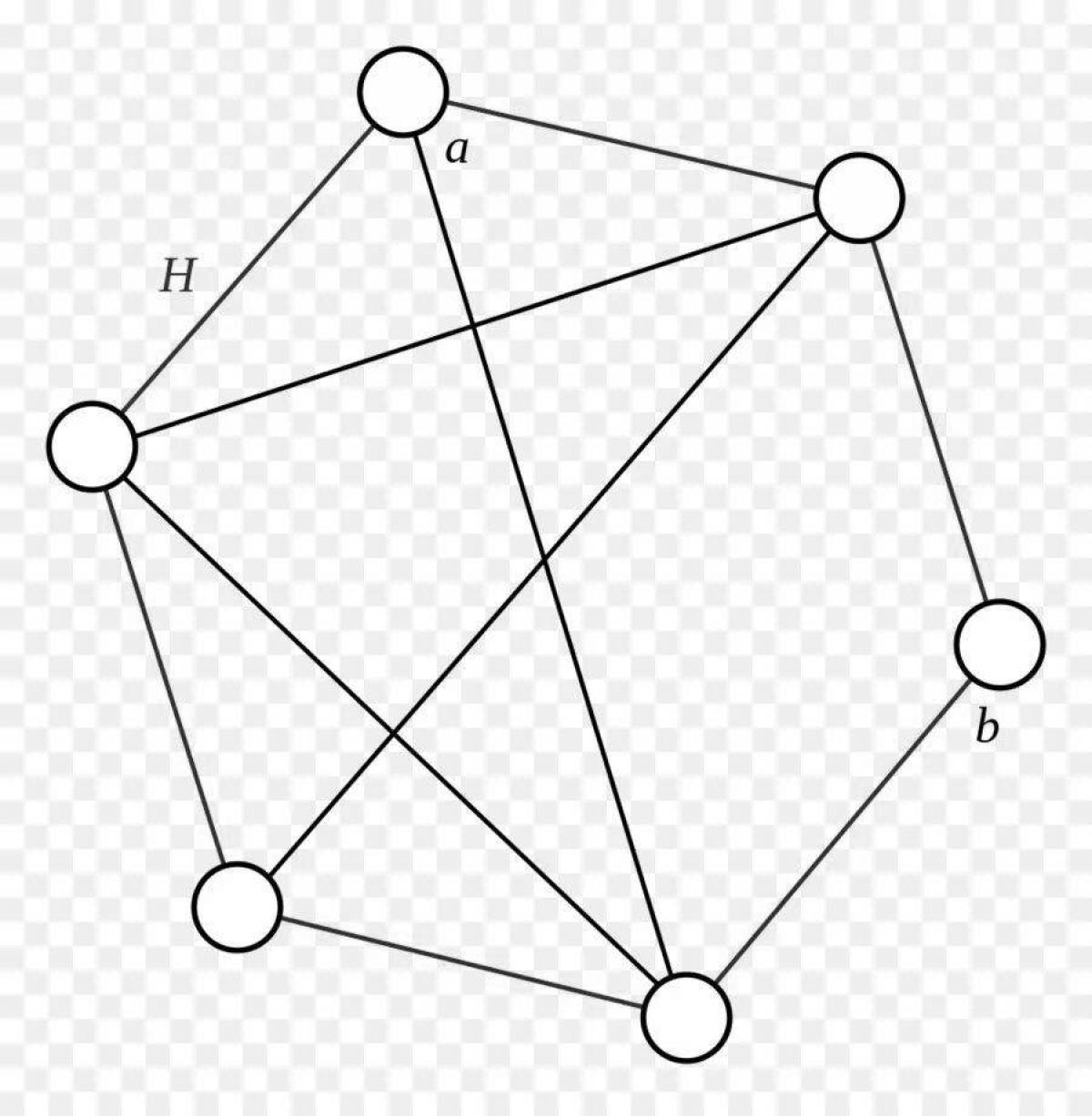
- Раскраской графа G в k цветов или k -раскраской называется разбиение элементов графа на k классов.
- При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин.
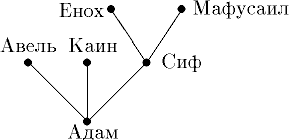









| 111 | Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину. | |
| 318 | Первоначально раскраски графов были нужны для составления географических карт [1]. Сегодня же они в частности раскраска с использованием минимального количества цветов используются, например, для составления расписаний, распределения регистров в микропроцессорах, распараллеливания численных методов. | |
| 179 | Нахождение фактора графа и остова графа для некоторого произвольного графа вершин Форумчане прошу помощь в выполнение задания по деск. | |
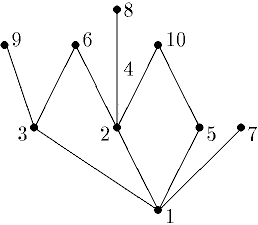
| 87 | Двудольные графы, критерий двудольности. | |
| 472 | Заметим, что рассуждение теоремы Форда — Фалкерсона фактически является алгоритмом нахождения максимального потока между двумя вершинами или доказательством того, что этот поток является максимальным. Подробный пример на эту тему также приведен в разделе «Решение типовых задач». | |
| 19 | Раскрашивать можно как ребра графа, так и вершины. Коснемся сначала задачи о раскраске вершин,. |
Категория: Математика. Похожие презентации:. Раскраска графов. Тема 3. Основные понятия.